ОКТАВА

 

 

 

                                                                          История квантовой эволюции была записана на языке чисел

                                в начальный момент образования нашей вселенной

 

                                                                        Тимоти Лири‚  История будущего

 

 

 

 

         Октава является основным музыкальным термином и  обозначает совпадение звуков‚ частоты которых со­относятся как 2:1. Вместе с тем  октава есть «восьмерица» (ὀκτώ - древнегреч.  «восемь»).

        

         Нетрудно понять‚ что основное свой­ство консонанса двух звуков с  от­ношением частот  2:1  заложено  в при­роде гармонической кривой: в полном  её периоде (2p) укладываются две полуфазы (p)‚ в двух полных периодах - четыре полуфазы и т.д.‚ что даёт при данном условии совпадение колебаний в фазовых точках:

 

 

 

                                       

                  

 

        

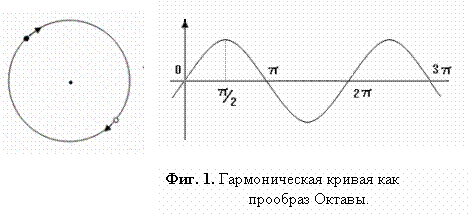
         Вместе с тем гармоническая кривая описывает простейший вид движения – осцилляцию‚ а математиче­ски является элементарной периодической функцией:   кривые других зависимостей могут быть разложены  в суммы  бесконечного ряда гармоник.

 

         Как же возникает в музыке разделе­ние интервала максимального консо­нанса  2 - октавы - на промежуточ­ные интервалы? Ответ на этот вопрос содер­жится в   древнейшей  из известных  истории систем музыкального строя - квинтовой‚ названной по имени Пифагора. Исторически  повелось‚ что корни всего могут быть найдены в Греции‚ однако же нет  оснований полагать‚ что       её принцип  не был извес­тен куда ранее в Египте‚ Вавилоне‚ Ин­дии и Китае.

         Колебания струны порождают частичные тоны (обертоны)‚  соотносящиеся как целые числа 1:2:3:4:5... Квинтовое деление основано на втором обертоне и сле­дующем за октавой консонансе  -  отношении частот  3:2.  Как доказывает  опыт со струнами различной длины‚ чем проще в числовом выраже­нии  это отношение‚ тем  приятнее их колебания на слух и полнее си­нергия (явление резонанса) между ними.

 

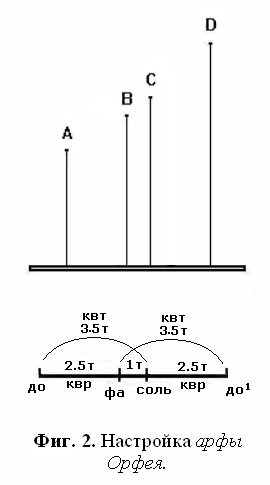
         Назовём октавный интервал  до-до¹. Ступень‚ относящаяся к тонике до по частоте как 3:2 на­зывается квинтой и традиционно обозна­чается  соль. Из определения интервала октавы следует‚ что отношение верх­него  до¹ к соль составит при этом 4:3‚ и это гармоническое отношение известно как кварта или обращённая квинта. Если заставить звучать три струны‚ настроен­ные в  до‚ соль и  до¹ одновременно‚  в аккорде будут присутствовать сразу три интервала - октава 2:1 ‚ квинта 3:2  и  кварта 4:3. Древние знали‚ что  квинта и кварта взаимообратимы - то есть сим­метричны в отношении  октавы‚ и если соль есть квинта к до‚ то фа - квинта к до¹‚ и  обратно -  фа  по отношению к до составляет  кварту‚ а соль - кварту к до¹.

         Эту пропорцию  можно представить в виде

                                                                                               до: фа: соль: до¹ = 1: 4/3 : 3/2 : 2‚

и она означает  первый гармонический паттерн октавы - так назы­ваемую на­стройку  орфеевой  арфы. Данное вы­ражение содер­жит в себе все  известные в древности отношения - а именно  ариф­метическую, геометри­ческую и гармони­ческую пропорции, а также принцип зо­лотого деления. Два его средних  члена при этом со­отно­сятся как  9:8‚ то есть обра­зуют  интервал  натурального целого тона - Фиг. 2. Таким образом‚  на­стройка арфы Орфея содержит алгоритм  (гномон)‚ посредством  которого на осно­вании отноше­ния  первых четырёх членов натурального ряда (греч. τετραξ - четве­рица)  могут быть установлены все  му­зыкальные сту­пени.

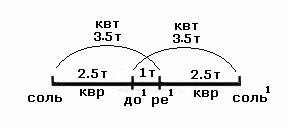
         Как это возможно? Последующее построение  есть хорошо знакомый  му­зыкантам  «квинтовый круг». Чтобы квинта первой четвёрки  в свою оче­редь  образовала октаву‚ достаточно изменить длину соответствующей струны вдвое.  Кварта в октаве  соль-соль¹ по-прежнему  до¹ ‚ а квинтой  ста­новится ступень ре¹:

                                                                                              Если фа  в октаве до - до¹ мы примем за  ступень со значе­нием 1‚ то   квинту от  фа   до¹ = 1 х 3/2 =  3/2  мы должны  понизить  вдвое‚ чтобы она пришлась в одну октаву с фа‚ совпав с тоникой до:

                                                                           до = 3/2 : 2 = 3/4.

         Тогда соль определяется как вторая квинта от значения

 до = 3/4:

                                               соль = 3/4 х 3/2 = 9/8.

Далее‚   ре¹ является  квинтой от соль:

                                               ре¹  = 9/8 х 3/2 = 27/16‚

и  величина 27/16 также должна быть уменьшена вдвое‚ поскольку вновь полученная ступень  превысила верхнюю границу  октавы до¹:

                                                                                                         ре = 27/16 : 2 = 27/32.

         Между до и ре - также как  между фа и соль – лежит интервал целого тона:                                                                                                                                                         27/32 : 3/4 = 9/8.

         Четвёртая по счёту квинта строится от ступени ре

                                                                                                        27/32  х 3/2= 81/64

и носит название ля‚ приходясь в ту же октаву: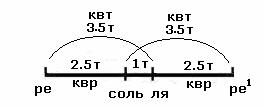                                        

         Между ля и  соль  интервал целого тона:

                                                                                              81/64 : 9/8 = 9/8.

         Пятая по счёту квинта (ми) строится от ля

                                                                                              81/64  х 3/2 = 243/128‚

и  должна быть приведена в одну октаву с ля:   

                                                                                     ми = 243/128 : 2 = 243/256.

                                                                                                                         

                  

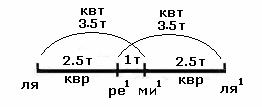
         Ми образует целотоновый про­межуток с ре:

                                                                                              243/256 : 27/32 = 9/8.

         Шестая по счёту квинта‚ которая строится от ноты ми и лежит в одной с ней октаве‚ называется си:

                                                                                               си = 243/256 х 3/2 = 729/512.

                                                                                                                         

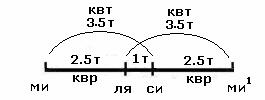
 Между  ля и си также  интервал целого тона

                                                                                      729/512  : 81/64  = 9/8.

 

 

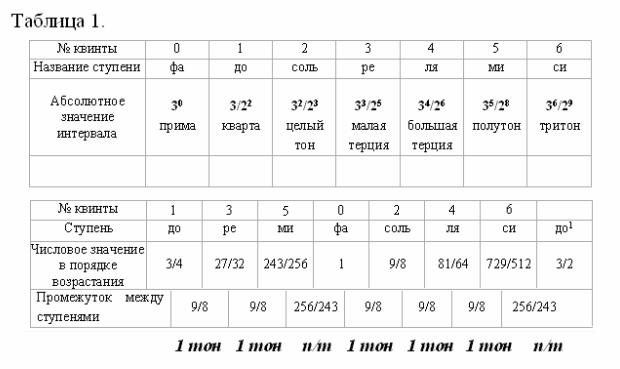
         Мы видим‚ что квинтовый алгоритм действует совершенно автоматически и единообразно. Сведём  вме­сте получен­ные резуль­таты - Таблица  1.

         Две последние квинтовые ступени  ми и си образовали новые интервалы внутри октавы:

                                                                           отношения фа / ми    1: 243/256 = 256/243

                                                                                     и       до¹ / си   3/4: 729/512  = 256/243

соответствуют  интервалу лейммы‚ называемой иначе полутоном.

          Леймма по-гречески «непроходи­мость»‚  и  означает прекраще­ние заполнения октавного промежутка интервалами в 1 тон. В самом деле‚ интервал 2 (октава) может вместить только 5 интер­валов 9/8  и 2 интервала 256/243:

                            (9/8)⁵ х (256/243)² = 2.

 

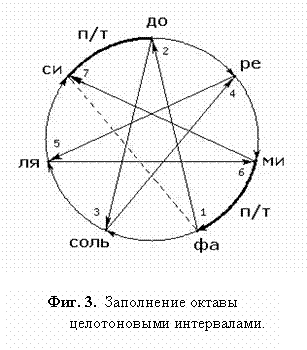
         Такое естественное заполнение октавного промежутка (2) тоновыми интервалами  с образо­ва­нием семиступенной по­следовательности  тон-тон-п/т-тон-тон-тон-п/т  называется  диатонической (мажор­ной) гаммой основных музыкальных ступеней:

 

 

  Шесть интервалов (3¹-3⁶) Таблицы 1‚ полученные 1-6 квинтами (а также обращения‚ дополняющие их  до октавы) содержат основу для всех музыкальных построений. Обращённая же прима (3⁰) соответствует самой октаве (2).

Продолжение квинтового алгоритма заставит  новые ступени «вклини­ваться» в тоновые промежутки ме­жду основными ступе­нями:

                              VII квинта есть 3⁶/2⁹ х 3/2 = 3⁷/2¹⁰, поскольку же она прихо­дится на вышележащую октаву (превышая значение до¹=3/2), это число  должно быть разделёно на 2,  что даёт 3⁷/2¹¹;

                              VIII квинта 3⁷/2¹¹х3/2=3⁸/2¹² >3/2,

 поэтому 3⁸/2¹²:2=3⁸/2¹³;

                              IX квинта  3⁸/2¹³х3/2=3⁹/2¹⁴;

                              X квинта   3⁹/2¹⁴х3/2=3¹⁰/2¹⁵>3/2,

                                                  поэтому 3¹⁰/2¹⁵:2=3¹⁰/2¹⁶;

                              XI квинта  3¹⁰/2¹⁶х3/2=3¹¹/2¹⁷;

                              XII квинта 3¹¹/2¹⁷х3/2=3¹²/2¹⁸>3/2,

                                                 поэтому 3¹²/2¹⁸:2=3¹²/2¹⁹.

 

         Все последующие ступени после первых семи (образованных с 0 по 6 квинту) обозначаются как изменённые (повышенные либо понижен­ные) основ­ные ступени. Седьмая квинтовая ступень ниже на полутон (2⁸/3⁵)  ступени  соль: 3²/2^{3 :} 2⁸/3⁵ =3⁷/2¹¹, поэтому она  называется соль-бемоль (соль^b). Восьмая квинта есть пониженная на пол­тона ре, так как 3³/2⁵:2⁸/3⁵=3⁸/2¹³‚ и соот­ветствует ре^b. Девятая, точно также – ля^b (3⁴/2⁶:2⁸/3⁵=3⁹/2¹⁴), десятая – ми^b (3⁵/2⁸:2⁸/3⁵=3¹⁰/2¹⁶), одиннадцатая – си^b (3⁶/2⁹:2⁸/3⁵=3¹¹/2¹⁷). Наконец, двенадцатая квинта приходится на по­ниженный на полтона интервал седьмой, по­скольку 3⁷/2¹¹ (соль^b) : 2⁸/3⁵=3¹²/2¹⁹. Сле­дуя принятому обозначению‚ мы должны отметить эту ступень как соль‚ дважды пониженное на  полтона  (соль^bb).

 

 

        

        

 

         В пифагорейском натураль­ном строе два полутона  (дубль-бемоль) не дают в сумме интер­вала, равного целому тону (2⁸/3⁵х2⁸/3⁵=2¹⁶/3¹⁰ <9/8)‚ поэтому последняя ступень не совпадает с фа №1 - не равна в точно­сти единице‚ то есть  ин­тервалу примы  (3¹²/2¹⁹=531441/524288 =1.0136432 >1)‚  превышая её на вели­чину пифагорейской коммы (обозначае­мой нами D).

 

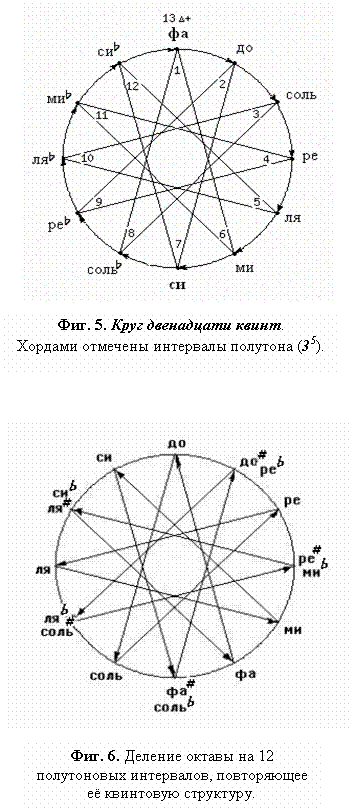         Следовательно‚ двенадцатая квинта вверх от исходной сту­пени  порож­дает новый  малый интервал 3¹²/2¹⁹ в фа № 13 (Фиг. 5)‚ чис­ленно соответствующий разнице  целого тона (9/8) с двумя полу­тонами 3²/2³:(2⁸/3⁵)²=3¹²/2¹⁹, что составляет при­мерно  1/8,69  целого тона (иначе говоря, 1.0136432^8,69 = 9/8). Образование микроинтервалов («комм») в квинтовом строе задаёт числовую основу системы натуральной микрохроматики. Полное заполнение интервала октавы полутоновыми ступенями даёт естественную (12-ти или 17-ти ступенную) хроматическую гамму. При этом восходящие квинты (по часовой стрелке круга) образуют ступени бемоля ()‚ а нисходящие (против часовой стрелки) - ступени диеза (#) - Фиг. 6‚ 7.

 

      

 

         Очевидно‚ что  на этом квинтовому процессу  не положен пре­дел. Если продол­жать его да­лее‚  все ступени квинтами вверх будут повторяться с повыше­нием на комму (+D) с каждым витком  спирали‚ и  при движении квинтами вниз (последова­тель­ные значения умножаются на 2/3‚ и также приводятся в исходную октаву) -  с убы­ванием (−D) в каждом цикле двенадцати.  Мы предоставляем проверить это самому чита­телю. Итеративное  деление отрезка  до - до¹ гармоническими числами бесконечно‚ и при этом  никогда не происходит совпадения положения  двух различных номеров.      

 

         Отметим основные моменты‚ инва­риантные относительно зна­чений ступеней‚ полученных  квинтовым алгоритмом - доста­точно‚ чтобы их номера шли по порядку*:

 

1.     каждые 12 последователь­ных ступеней  образуют нату­ральную хро­матическую гамму с подразделением октавы на 12 полутонов- Фиг. 6;

 

2. 17 последовательно взятых ступеней образуют семнадцати­ступенную хроматическую гамму 12-ти полутонов с энгармонически неравными повышенными и пони­женными ступенями‚ разделён­ными  интервалами  коммы (D) - Фиг. 7;

 

 3.  каждая тринадцатая ступень в периоде 12-ти квинт замыкает октавный цикл‚ порож­дая  сдвиг на микротоновый интер­вал (комму D) - Фиг. 5;

 

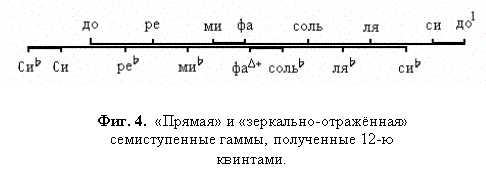
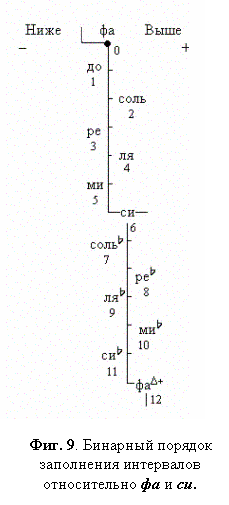
4.  каждый диаметр‚ проведённый через  противолежащие ступени  двенадцатичленного круга‚ отме­чает  в нём ось зеркальной симметрии  и  два  полюса‚ относи­тельно которых проявлен двоичный паттерн Октавы - Фиг. 4‚9;

 

5.     каждые 7 следующих по порядку ступеней‚ отделённых диаметром (Фиг. 10) образуют семиступенную гамму с пятью целото­новыми  и двумя полутоновыми про­межутками одного из семи принятых в антично­сти ладов (либо заменяющей лад тональности)  - се­меричный  паттерн Октавы:

                      

                                                                 

 

                                                                                                    

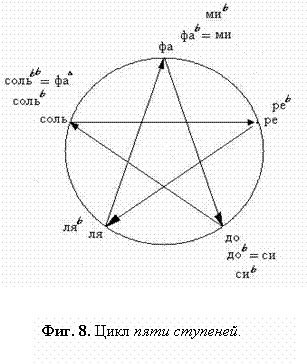
6.  все вышеуказанные свой­ства  Октавы определены её пя­теричным  циклом:   пять  квинт вверх результируют по­нижением исходной ступени на пол­тона‚  либо повышением на полтона при движении квинтами вниз - Фиг. 5‚ 8;

 

7.  далее‚ двенадцатеричный поря­док  разбивается на  «квадранты» и «тригоны»  малой и боль­шой терций‚ служащих в музыке основой  аккордово-гармонических построений - Фиг. 11;

 

8.  и‚ наконец‚ все описанные  от­ношения проистекают из начал чёта и нечёта         (3ⁿ : 2^m)‚ заложенных в квинтовый алгоритм.  Свойства Октавы как умозрительного объекта  не зависят от природы звука‚ и вправе  рассматриваться  как  проявление законов числа. Подобные принципы числовой организации обнаруживаются и в ДНК – универсальном коде жизни.

 

 

 

 

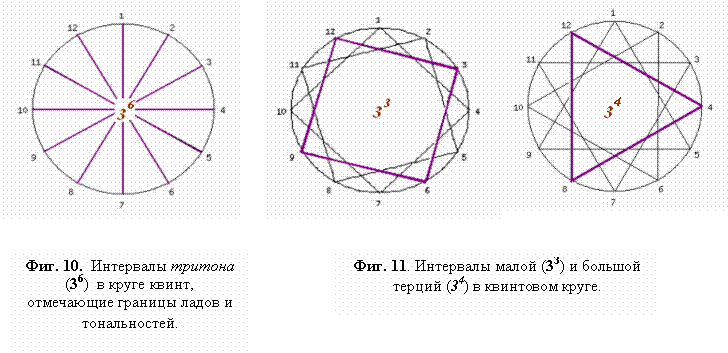
         Присутствие коммы в квинтовом  круге было известно издавна и служило постоянным раздражающим фактором для музыкальных теоре­тиков. Им казалось  неудобным образование в натуральном строе тональных гамм с комматически смещён­ными ступенями‚ а также и то‚ что октава не замкнута - два натуральных полутона не образуют в точности  целый тон. Уже греческий философ Аристоксен‚ ученик  Аристотеля (IV в. до н.э.)‚ предложил  темперированный  строй -  деление октавы на равные интервалы. Но эта рационалистическая идея смогла осуществиться лишь во второй половине XVII века‚ когда каждый полутон объявили равным ровно 100 центам‚ или .

 

         Это дало возмож­ность‚ бесконечно поднимаясь по лестнице квинт‚ неизменно возвращаться к её началу‚ -  как мы видим на гравюре  Маурица  Эшера  и  в чём  убеждают нас органные произведения  Иоганна-Себастьяна Баха - Рис.1.

         Но  те‚ кто стоял ближе к основаниям квинтовой системы‚ не могли не сознавать её фрактальные возмож­ности -  об этом свидетельствуют известные места платонова Тимея (36).

         Продолжим итерации виток за витком двенадцатиступенного круга. Нетрудно убедиться‚ что на пятом круге будет достигнуто приращение в 4 коммы‚ что превышает интервал полутона (3.85 D). Тогда ступень  12х4+6 = №54  ми станет на полтона выше‚ то есть «обратится» в  фа‚ а «квинтовая спираль» пересечёт самое себя во второй раз - первое сближение мы видели в №13. На сей раз‚ показывает расчёт‚ «соединение» более полное – новый микроинтервал (s) в 6.5 раз меньше пифагорейской коммы (D)‚ а  «витки спирали» стали зна­чительно шире.

         Отправляясь от нового значения‚ мы вправе ожидать‚ что на седьмом круге цикла в 53 квинты s-прираще­ния достигнут величины D‚ и снова произойдёт «соединение» с единичным фа. При этом  ступень №54 + 53 х 6 = 372 достигнет  (и превысит ещё на какое-то микротональное деление) величину сту­пени №13 фа^D. Если №13 приходит в соответствие с № 372‚ то №1‚ очевидно‚ отвечает  372─12 = № 360‚ так что следующее «возвраще­ние»  происходит ровно на этом номере‚ что подтверждается компьютерным моделированием пифагорейских гармонических чисел.

         Не боясь наскучить читателю‚ мы не откажем себе в удовольствии привести расчёт «на пальцах» и следую­щего соединения. Поскольку интервал ок­тавы 2 содержит 51 микротон I порядка D плюс один мик­ротон II порядка s‚ то приращение комм D с каждым циклом 12-ти ступеней за 51х12=612 номе­ров покроет интервал в 51D‚ а для получения малого приращения s‚ как мы знаем‚ нужен ещё период в 53 ступени. Приба­вив к №1фа 51 цикл по 12 но­меров и один в 53 номера‚ мы  получим искомое значение ступени  №1+612+53 = №666 - самое близкое после единицы среди более чем 16000  гармонических чисел (этот микроинтервал  t  состав­ляет 1/15878  часть октавы) - Фиг. 12. Так‚ занимаясь  вроде  вполне безобидным делом‚  мы  невзначай  затронули  «эсхатологическую» тему.

 

         54 есть сумма  «двойных и  тройных чисел»‚ приводимых  Тимеем  как принцип  расчленения Октавы  космоса:

 

                                                                                 

 

 

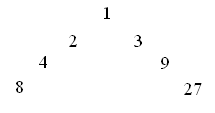
         360  тоже  хорошо известно -  до сих пор так считают градусы окружности‚ но причём здесь «число Антихриста»? Ответ может заключаться в том‚ что 666 не менее других паттернов Октавы пригодно для представления временнх циклов‚ ведь

 

                            «устрояя  небо, Он  творит... вечный  же образ, движу­щийся от числа к числу, который мы назвали временем»

                                                                                              (Тимей‚ 36b).

 

         Время - «материя» столь же привычная для нас‚ сколь и непонятная‚ - по свидетельству всех мистиков‚ есть принцип фрактального раздробления единого Бытия.

 

         Каждый из  периодов Октавы отвечает гамме с соответствующим микротональным делением‚ поддержи­вая основное фрактальное свойство - создавать циклы внутри циклов‚ повторяя одни и те же  числовые узоры в нисходящем порядке шкалы масштабов‚ -  возьмём для примера известное множество Мандельбро.  В этом смысле мы можем говорить о «внутренних октавах»*‚ вкладываемых друг в друга наподобие матрёшек. Период в 665 квинт выступает при этом характерным аттрактором‚ повторяющим  в своём интервале исходный рисунок двена­дцати сту­пеней -  Фиг. 13 а‚б:

 

 

                                                                 

                  

                                                                          

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

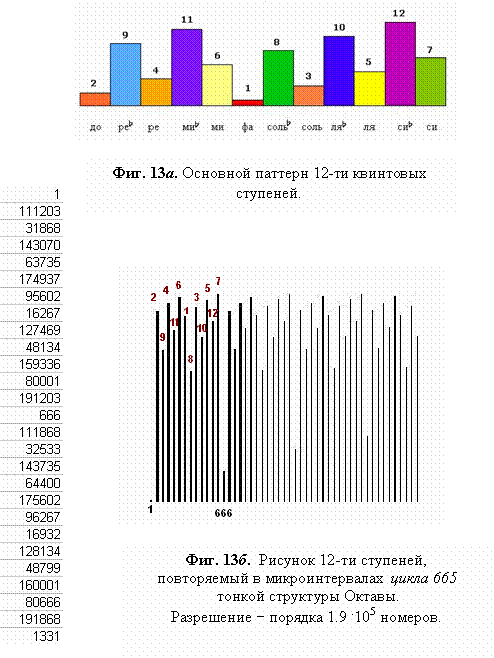
Периоды более высоких порядков раскладываются на нижележащие как на составляющие модули‚ свя­зующим  звеном  выступает  цикл 665:

 

                                                        16266    =    665   х  24  +  359 ─ 53‚

                                                        31867    =  16266  х   2  ─   665‚

                                                        79335    =  16266  х   5  ─  665  х  3‚

                                                        111202  =  16266  х   7  ─  665  х  4‚

                                                        190537  =  16266  х  12 ─  665  х   7‚ 

                                                        301739  =  16266  х  19 ─  665  х  11‚   и т.д.

 

Ранее период 665 был нами получен из 53 и 12 (12 х 51+53 = 665)‚ а 53 точно также следует из 12 и 5 (12 х 4 + 5 = 53). Все они приводят обратно к тетраксу (1:2:3:4)‚ определённому нами выше в качестве основной октавной структуры. Такого рода «сквозной» принцип фрактальной организации мы видим и в натуральном золотом ряде чисел Фибоначчи  - и‚ как знать‚ все «большие числа» математики и физики‚ быть может‚ в конечном итоге сводятся к немногим фундаментальным «кирпичикам»‚ как это утверждали пифагорейцы?

 

 

В конце  XVI века  француз Жозеф Скалигер задумал создать времяисчисление‚ наилучшим образом со­гласованное с известными на то время астрономическими и историческими данными‚ и   предложил так назы­ваемый юлианский период в 7980 лет‚  попав как раз «в яблочко»‚ поскольку эра Скалигера - до сих пор‚ кстати‚  используемая при хронологических расчётах‚ -  как раз основана на  периоде 665  (7980 = 665 х 12).

Вряд ли Скалигер‚ да и Св. Иоанн опирались на  непосредственное знание об Октаве‚ но её следы уводят куда дальше.  Носящая имя Пифагора квинтовая система по глубине своей общности является бессмертным памятником - а равно и универсальным кодом человечества: если даже предположить‚ что знание о ней было бы когда-либо утрачено‚ её неизбежно переоткрыли бы снова. Странные «мистические»  принципы‚ положенные древними в основание природы и применённые в философии‚ астроло­гии и счёте времени - пара инь-ян‚ три гуны‚ пять элементов‚ восемь направлений и двенадцать знаков Зодиака‚ шестидесятилетний цикл‚ загадочный И цзин‚ майанский календарь и древнеиндийские эры - все они так или иначе находят в Октаве свой прообраз.

 

 

 

 

 

                            Главная страница

 

2005 © Б.Сварог

         waruna@yandex.ru